Kondensatora kapacitātes aprēķins

Kapacitāte C ir kondensatora spēja pieņemt (uzglabāt un noturēt) elektroenerģijas daudzumu Q ampērsekundēs vai lādiņu Q piekariņos. Ja kādam ķermenim, piemēram, lodei, pasaka elektrisko lādiņu (elektrības daudzumu) Q, tad starp šo ķermeni un zemi savienotais elektroskops parādīs spriegumu U (1. att.). Šis spriegums ir proporcionāls lādiņam un ir atkarīgs arī no ķermeņa formas un izmēra.

Sakarību starp lādiņu Q un spriegumu U izsaka ar formulu Q = C ∙ U.

Proporcionalitātes konstanti C sauc par ķermeņa kapacitāti. Ja ķermenim ir bumbiņas forma, ķermeņa kapacitāte ir proporcionāla lodes rādiusam r.

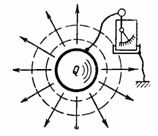
Rīsi. 1.

Kapacitātes mērvienība ir farads (F).

Ķermeņa kapacitāte ir 1 F, kad lādiņš 1 k rada spriegumu 1 V. starp to un zemi. Farādes ir ļoti liela mērvienība, tāpēc praksē tiek izmantotas mazākas mērvienības: mikrofarāde (μF), nanofarāde (nF) un pikofarāde (pF)...

Šīs vienības ir saistītas ar šādām attiecībām: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Bumbiņas kapacitāte ar rādiusu 1 cm ir 1,1 pF.

Ne tikai izolēts ķermenis var uzkrāt lādiņu, bet arī īpaša ierīce, ko sauc par kondensatoru. Kondensators sastāv no divām vai vairākām plāksnēm (plāksnēm), kuras atdala ar dielektriķi (izolāciju).

attēlā. 2 parāda ķēdi ar līdzstrāvas avotu, kas savienots ar kondensatoru. Ieslēdzot, kondensatora labajā plāksnē veidojas pozitīvs lādiņš +Q un kreisajā plāksnē negatīvs lādiņš –Q. Laikā kondensatora lādiņš caur ķēdi plūst strāva, kas apstājas pēc uzlādes beigām; tad spriegums pāri kondensatoram būs vienāds ar e. utt. c) avots U. Kondensatora plāksnes lādiņš, spriegums un kapacitāte ir saistīti ar attiecību Q = C ∙ U. Šajā gadījumā kondensatora dielektrikā veidojas elektrostatiskais lauks.

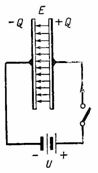
Rīsi. 2.

Kondensatora ar gaisa dielektriķi jaudu var aprēķināt pēc formulas C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, kur S ir vienas plāksnes laukums, cm2; d ir attālums starp plāksnēm, cm; C ir kondensatora kapacitāte, pF.

Kondensatora, kas sastāv no n plāksnēm (3. att.), jauda ir vienāda ar: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

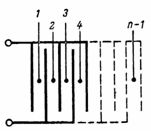
Rīsi. 3.

Ja vietu starp plāksnēm piepilda ar citu dielektriķi, piemēram, papīru, kondensatora kapacitāte palielināsies par ε. Izmantojot papīra izolāciju, jauda palielināsies 3 reizes, ar vizlas izolāciju - 5-8 reizes, ar stiklu - 7 reizes utt. Vērtību ε sauc par dielektriķa dielektrisko konstanti.

Vispārējā formula kondensatora kapacitātes noteikšanai ar dielektrisko konstanti ε (epsilons) ir: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Šī formula ir noderīga, lai aprēķinātu mazus mainīgus radioaparātu kondensatorus.To pašu formulu var attēlot šādi: C = (ε_0 ∙ ε ∙ S) / d, kur ε_0 ir vakuuma dielektriskā konstante vai dielektriskā konstante (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε ir dielektriķa dielektriskā konstante.

Šajā formulā izmēri tiek aizstāti metros, un kapacitāte tiek iegūta farados.

Piemēri

1. Kāda ir planētas Zeme kapacitāte, kuras rādiuss ir r = 6378 km?

Tā kā sfēras kapacitāte ar rādiusu 1 cm ir vienāda ar 1,11 pF, tad Zemes kapacitāte ir: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μ. (Mūsu planētas izmēra bumbiņas kapacitāte ir salīdzinoši maza. Maza izmēra elektrolītiskajiem kondensatoriem ir šāda jauda).

2. Nosakiet kondensatora kapacitāti, kas sastāv no divām plāksnēm, no kurām katras laukums ir S = 120 cm2.

Plāksnes atdala gaisa slānis, kura biezums ir d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Nosakiet kondensatora kapacitāti ar iepriekšējā piemērā dotajiem datiem, ja atstarpi starp plāksnēm piepilda ar vaska papīru ar dielektrisko konstanti ε = 4, stiklu (ε = 7), elektrisko kartonu (ε = 2) , vizla (ε = 8).

Vaska papīra kondensatora kapacitāte C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Stikla kondensatora kapacitāte ir C = 7 ∙ 21,2 = 148,4 pF.

Kartona kondensatora kapacitāte ir C = 2 ∙ 21,2 = 42,3 pF.

Vizlas kondensatora kapacitāte ir C = 8 ∙ 21,2 = 169,6 pF.

4. Kāda ir gaisa rotācijas kondensatora kapacitāte radio uztvērējam, kas sastāv no 20 plāksnēm ar laukumu 20 cm2, ja attālums starp plāksnēm ir 0,06 cm (149. att.)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Attēlā parādītais kondensators.3, sastāv no atsevišķiem vienkāršākajiem kondensatoriem ar divām plāksnēm, kuru skaits ir vienāds ar n-1.

5. Papīra kondensators ar kapacitāti C = 2 μF sastāv no divām alvas folijas sloksnēm C un divām dielektriķa sloksnēm, kas izgatavotas no vaska papīra B ar dielektrisko konstanti ε = 6. Vaska papīra biezums ir d = 0,1 mm. Salocītās sloksnes ir sarullētas, vadi ir izgatavoti no tērauda plāksnēm. Nosakiet kondensatora tērauda sloksnes garumu, ja tās platums ir 4 cm (4. att.).

Rīsi. 4.

Pirmkārt, mēs nosakām vienas sloksnes laukumu pēc formulas C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, no kurienes S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Katras sloksnes garums ir l = 37680/4 = 9420 cm = 94,2 m.