Rezultātā esošās pretestības aprēķins virknes-paralēlā savienojumā

Jēdzieni un formulas

Sērijas paralēlais vai jauktais savienojums ir trīs vai vairāku pretestību komplekss savienojums. Jauktā savienojuma rezultātā iegūtā pretestība tiek aprēķināta pa posmiem, izmantojot formulas pretestības aprēķināšanai virknē un paralēlu savienojumu.

Piemēri

1. Aprēķiniet trīs pretestību virknes paralēlo savienojumu pēc diagrammas att. 1.

Vispirms nomainiet paralēli savienotās pretestības r2 un r3 ar iegūto pretestību r (2-3):

r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 omi.

Rezultātā visas ķēdes pretestība ir r = r1 + r (2-3) = 5 + 6,6 = 11,6 omi.

Rīsi. 1.

2. Kāda strāva plūst caur ķēdi (2. att.) atvērtā un slēgtā gadījumā naža slēdzis P? Kā mainās spriegums pāri pretestībai r2 abos gadījumos?

Rīsi. 2.

a) Slēdzis ir atvērts. Sērijveidā savienoto pretestību r1 un r2 rezultējošā pretestība

r (1-2) = r1 + r2 = 25 omi.

Strāva I (1-2) = U / r (1-2) = 100/25 = 4 A.

Sprieguma kritums pāri pretestībai r2

U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V.

b) Slēdzis ir aizvērts. Paralēli savienoto rezistoru r1 un r3 rezistoru pretestība

r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 omi.

Visas ķēdes kopējā pretestība ir r = r (1-3) + r2 = 6,6 + 5 = 11,6 omi.

Strāva I = U / r = 100 / 11,6 = 8,62 A.

Sprieguma kritums uz pretestības r2 šajā gadījumā ir vienāds ar: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.

Otrajā gadījumā strāva palielinājās paralēlās pretestības R3 pieslēgšanas rezultātā. Vairāk strāvas rada vairāk sprieguma kritums pie pretestības r2.

3. Kādam jābūt papildu pretestība rd, lai divas paralēli pieslēgtas lampas 120 V spriegumam un 0,2 A strāvai varētu pieslēgt tīklam ar spriegumu U = 220 V (3. att.)?

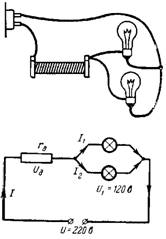
Rīsi. 3.

Spriegumam lampās jābūt vienādam ar 120 V. Atlikušais spriegums (100 V) nokrīt uz papildu pretestības rd. Caur pretestību rd plūst divu lukturu strāva I = 0,4 A.

Saskaņā ar Oma likumu rd = Ud / I = 100 / 0,4 = 250 Ohm.

4. Elektroniskās lampas ar 1,2 V kvēldiegu un kvēldiega strāvu 0,025 un 0,05 A ir virknē savienotas ar līdzstrāvas avotu ar spriegumu 4,5 V. Kādai jābūt papildu pretestībai rd un paralēlā pretestība (šunts) uz lampu ar mazāku kvēldiega strāvu (4. att.)?

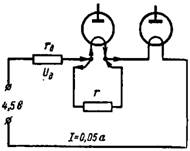
Rīsi. 4.

Pretestības ķēdē ir jāizvēlas tā, lai otrās lampas kvēldiega strāva plūst I = 0,05 A. Spriegums pāri elektronisko spuldžu kvēldiegam būs 1,2 + 1,2 = 2,4 V. Atņemot šo vērtību no akumulatora sprieguma, mēs ņem sprieguma krituma vērtību pāri papildu pretestībai rd: Ud = 4,5-2,4 = 2,1 V.

Tāpēc papildu pretestība rd = (Ud) / I = 2,1 / 0,05 = 42 omi.

Kvēldiega strāvai 0,05 A nevajadzētu plūst cauri pirmās vakuuma caurules kvēldiegam. Pusei no šīs strāvas (0,05-0,025 = 0,025 A) jāiet cauri šuntam r. Šunta spriegums ir tāds pats kā lampas kvēldiegam, t.i. 1,2 V. Tāpēc šunta pretestība ir: r = 1,2 / 0,025 = 48 omi.

5. Kāda ir iegūtā ķēdes pretestība un tajā esošā strāva ķēdē attēlā. 5?

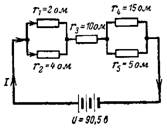
Rīsi. 5.

Vispirms noteiksim paralēli savienoto rezistoru iegūto pretestību:

r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 omi;

r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 omi.

Iegūtā ķēdes pretestība ir:

r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 omi.

Iegūtā strāva pie sprieguma U = 90,5 V

I = U / r = 90,5 / 15,05 = 6 A.

6. Aprēķiniet sarežģītā virknes-paralēlā savienojuma iegūto pretestību fig. 6. Aprēķiniet iegūto strāvu I, strāvu I4 un sprieguma kritumu pāri pretestībai r1.

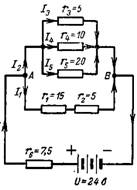
Rīsi. 6.

Paralēli savienoto pretestību rezultātā iegūtā vadītspēja

1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;

r (3-4-5) = 20/7 = 2,85 omi.

R1 un r2 ķēdes pretestība ir:

r (1-2) = r1 + r2 = 15 + 5 = 20 omi.

Iegūtā vadītspēja un pretestība starp punktiem A un B ir attiecīgi vienādas: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 omi.

Rezultātā visas ķēdes pretestība ir r = rAB + r6 = 2,5 + 7,5 = 10 omi.

Iegūtā strāva ir I = U / r = 24/10 = 2,4 A.

Spriegums starp punktiem A un B ir vienāds ar avota spriegumu U mīnus sprieguma kritums pāri rezistoram r6

UAB = U-I ∙ r6 = 24-(2,4 ∙ 7,5) = 6 V.

Pretestība r4 ir pievienota šim spriegumam, tāpēc strāva caur to būs vienāda ar:

I4 = UAB / r4 = 6/10 = 0,6A.

Rezistoriem r1 un r2 ir kopīgs sprieguma kritums UAB, tāpēc strāva caur r1 ir:

I1 = UAB / r (1-2) = 6/20 = 0,3 A.

Sprieguma kritums pāri pretestībai r1

Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.

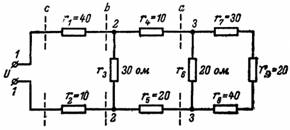
7. Kāda ir iegūtā pretestība un strāva att. ķēdē. 7, ja avota spriegums ir U = 220 V?

Rīsi. 7.

Mēs sākam ar ķēdi, kas atrodas pa labi no mezgliem 3 un 3. Pretestības r7, r8, r9 ir savienotas virknē, tāpēc

r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 omi.

Paralēli šai pretestībai ir savienota pretestība r6, tāpēc iegūtā pretestība mezglā 3 un 3 (a sadaļa)

ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 omi.

Pretestības r4 un r5 ir savienotas virknē ar pretestību ra:

r (4-5-a) = 10 + 20 + 16,36 = 46,36 omi.

2. un 2. mezglu rezultējošā pretestība (b sadaļa)

rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46,36 ∙ 30) / (46,36 + 30) = 1390,8 / 76, 36 = 18,28 omi.

Iegūtā visas ķēdes pretestība ir r = r1 + rb + r2 = 40 + 18,28 + 10 = 68,28 omi.

Iegūtā strāva ir I = U / r = 220 / 68,28 = 3,8 A.