Magnētiskā lauka mērīšanas principi, instrumenti magnētiskā lauka parametru mērīšanai

Pirmie magnētiskie kompasi, kas norāda virzienus uz Zemes magnētiskajiem poliem, parādījās trešajā gadsimtā pirms mūsu ēras Ķīnā. Tās bija no magnētiskās dzelzsrūdas izgatavotas ierīces apaļu kausu veidā ar īsu rokturi.

Karoti ar savu izliekto daļu novietoja uz gludas vara vai koka virsmas, uz kuras tika uzzīmēti dalījumi ar zodiaka zīmju attēliem, norādot kardinālos punktus. Lai aktivizētu kompasu, karote tika viegli nospiesta un tā sāka griezties. Galu galā, kad karote apstājās, tās rokturis bija vērsts tieši tā virzienā uz Zemes dienvidu magnētisko polu.

Kopš divpadsmitā gadsimta ceļotāji Eiropā aktīvi izmantoja kompasus. Tie tika uzstādīti gan uz sauszemes transporta, gan jūras kuģiem, lai noteiktu magnētisko novirzi.

Kopš astoņpadsmitā gadsimta beigām magnētiskās parādības kļuva par tā laika zinātnieku rūpīgas izpētes objektu. Kulons 1785. gadā ierosināja metodi Zemes magnētiskā lauka stipruma kvantitatīvai noteikšanai. 1832. gadāGauss parādīja iespēju noteikt magnētiskā lauka intensitātes absolūto vērtību, izmantojot precīzākus mērījumus.

Saikni starp magnētiskajām parādībām un spēka efektiem, kas novēroti elektrisko lādiņu kustības laikā, pirmo reizi noskaidroja Oersteds 1820. gadā. Maksvels vēlāk uzrakstīja šo attiecību racionālā formā - matemātisko vienādojumu veidā (1873):

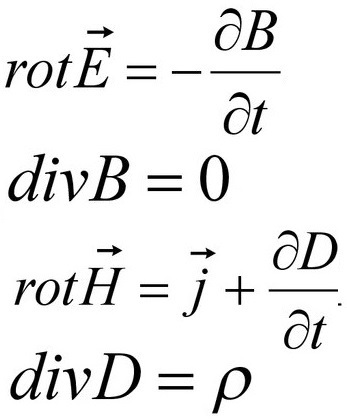
Līdz šim magnētiskā lauka parametru mērīšanai tiek izmantota šāda metode:

• teslametri - ierīces spēka H vērtību vai magnētiskā lauka B indukcijas mērīšanai;

• webmetri — instrumenti magnētiskās plūsmas Ф lieluma mērīšanai;

• gradiometri — ierīces magnētiskā lauka neviendabīguma mērīšanai.

pastāv arī:

• ierīces magnētiskā momenta M mērīšanai;

• instrumenti vektora B virziena mērīšanai;

• instrumenti dažādu materiālu magnētisko konstantu mērīšanai.

Magnētiskās indukcijas vektors B raksturo spēcīgas blakusdarbības intensitāti magnētiskais lauks (uz polu vai strāvu), un tāpēc tas ir tā galvenais raksturlielums noteiktā telpas punktā.

Tādējādi pētāmais magnētiskais lauks var spēcīgi mijiedarboties vai nu ar magnētu, vai ar strāvas elementu, kā arī spēj izraisīt indukcijas EML ķēdē, ja magnētiskais lauks, kas iekļūst ķēdē, laika gaitā mainās vai ja ķēdes stāvoklis mainās attiecībā pret magnētiskais lauks.

Uz strāvu nesošo elementu ar garumu dl indukcijas B magnētiskajā laukā iedarbosies spēks F, kura vērtību var atrast, izmantojot šādu formulu:

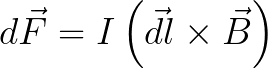
Tāpēc pētāmā magnētiskā lauka indukciju B var atrast ar spēku F, kas iedarbojas uz dotā garuma l vadītāju ar zināmas vērtības I līdzstrāvu, kas novietots šajā magnētiskajā laukā.

Praksē magnētiskos mērījumus ērti veikt, izmantojot lielumu, ko sauc par magnētisko momentu. Magnētiskais moments Pm raksturo apgabala S kontūru ar strāvu I, un magnētiskā momenta lielumu nosaka šādi:

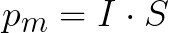
Ja tiek izmantota spole ar N apgriezieniem, tad tās magnētiskais moments būs vienāds ar:

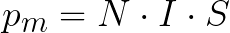
Magnētiskās mijiedarbības spēka mehānisko momentu M var atrast, pamatojoties uz magnētiskā momenta Pm un magnētiskā lauka indukcijas B vērtībām šādi:

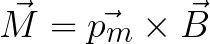
Tomēr, lai izmērītu magnētisko lauku, ne vienmēr ir ērti izmantot tā mehāniskā spēka izpausmes. Par laimi, ir vēl viena parādība, uz kuru varat paļauties. Šī ir elektromagnētiskās indukcijas parādība. Elektromagnētiskās indukcijas likums matemātiskā formā ir uzrakstīts šādi:

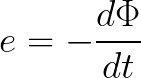
Tādējādi magnētiskais lauks izpaužas kā spēki vai izraisīts EML. Šajā gadījumā pats magnētiskā lauka avots, kā zināms, ir elektriskā strāva.

Ja ir zināma strāva, kas rada magnētisko lauku noteiktā telpas punktā, tad var atrast magnētiskā lauka stiprumu šajā punktā (attālumā r no strāvas elementa). izmantojot Biota-Savarta-Laplasa likumu:

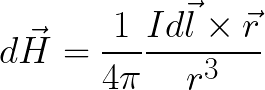
Jāņem vērā, ka magnētiskā indukcija B vakuumā ir saistīta ar magnētiskā lauka intensitāti H (ko rada atbilstošā strāva) ar šādu attiecību:

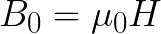
Vakuuma magnētiskā konstante SI sistēmā ir noteikta ampēros.Patvaļīgai videi šī konstante ir magnētiskās indukcijas attiecība noteiktā vidē pret magnētisko indukciju vakuumā, un šo konstanti sauc barotnes magnētiskā caurlaidība:

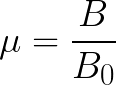
Gaisa magnētiskā caurlaidība praktiski sakrīt ar vakuuma magnētisko caurlaidību; tāpēc gaisam magnētiskā indukcija B ir praktiski identiska magnētiskā lauka spriegumam H.

Mērvienība magnētiskās indukcijas mērīšanai ZA — Tesla [T], CGS sistēmā — Gauss [G], un 1 T = 10000 G. Mērierīces magnētiskā lauka indukcijas noteikšanai sauc par teslametriem.

Magnētiskā lauka stiprumu H mēra ampēros uz metru (A/m), un 1 ampērs/metrs tiek definēts kā bezgalīga garuma solenoīda magnētiskā lauka stiprums ar vienības pagrieziena blīvumu, kad caur to plūst 1 ampēra solenoīda strāva. Vienu ampēru uz metru var definēt citā veidā: tas ir magnētiskā lauka stiprums apļveida ķēdes centrā ar strāvu 1 ampērs ar cilpas diametru 1 metrs.

Šeit ir vērts atzīmēt tādu vērtību kā indukcijas magnētiskā plūsma — F. Tas ir skalārs lielums, SI sistēmā to mēra Vēberā, bet CGS sistēmā — Maksvelsā ar 1 μs = 0,00000001 Wb. 1 Vēbers ir tāda lieluma magnētiskā plūsma, ka tad, kad tā samazinās līdz nullei, 1 kulona lādiņš iziet cauri vadošai ķēdei, kuras pretestība ir 1 Ohm.

Ja par sākotnējo vērtību ņemam magnētisko plūsmu F, tad magnētiskā lauka indukcija B būs nekas cits kā magnētiskās plūsmas blīvums. Magnētiskās plūsmas mērīšanas ierīces sauc par tīmekļa mērītājiem.

Iepriekš mēs atzīmējām, ka magnētisko indukciju var noteikt vai nu ar spēku (vai ar mehānisko momentu), vai ar ķēdē inducēto EML. Tās ir tā sauktās tiešās mērījumu pārvēršanas, kur magnētisko plūsmu vai magnētisko indukciju izsaka ar citu fizisko lielumu (spēku, lādiņu, momentu, potenciālu starpību), kas ir unikāli saistīts ar magnētisko lielumu, izmantojot fizisko pamatlikumu.

Transformācijas, kurās magnētiskā indukcija B vai magnētiskā plūsma F ir caur strāvu I vai garumu l vai rādiusu r, sauc par reversajām transformācijām. Šādas transformācijas tiek veiktas, pamatojoties uz Biota-Savarta-Laplasa likumu, izmantojot zināmo saistību starp magnētisko indukciju B un magnētiskā lauka H stiprumu.