Shēmu topoloģijas — pamatjēdzieni

Elektriskā ķēde ir ierīču (elementu) un to savienojošo vadu kopums, caur kuru var plūst elektriskā strāva. Visi elektrisko ķēžu elementi ir kopīgi pasīvajā un aktīvajā.

Aktīvie elementi pārvērš dažāda veida enerģiju (mehānisko, ķīmisko, gaismas utt.) elektroenerģijā. Pasīvās ierīcēs elektriskā enerģija tiek pārveidota par cita veida enerģiju. Aktīvos elementus sauc par avotiem, pasīvos par patērētājiem vai uztvērējiem.

Ķēdes teorijā tiek aplūkoti idealizēti elektrisko elementu modeļi. Tas padara elementu aprakstu pēc iespējas vienkāršāku. Sarežģītāki, reāli elementi tiek modelēti no idealizētu elementu kopas.

Galvenie elektrisko ķēžu pasīvie elementi ir rezistors (rezistīvais elements), induktors (induktīvais elements) un kondensators (kapacitatīvs elements). Elementi ir uzstādīti elektriskajā ķēdē, lai radītu noteiktas vērtības un formas spriegumu un strāvu (sk. Elektriskā ķēde un tās elementi).

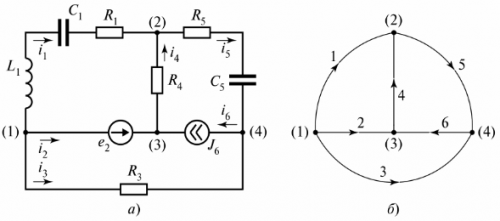
Elektriskā ķēde sastāv no zariem un mezgliem. Filiāle — šī ir elektriskās ķēdes (ķēdes) daļa, caur kuru plūst viena un tā pati strāva. Mezgls — trīs vai vairāku atzaru savienojums. Elektriskajā shēmā mezgls ir norādīts ar punktu (1. att.).

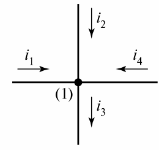
Rīsi. 1. Diagrammā definējiet mezglu

Ja nepieciešams, diagrammas mezglus numurē no kreisās puses uz labo no augšas uz leju.

attēlā. 2 parāda rezistīvi-kapacitatīvo atzaru, kurā plūst strāva iC.

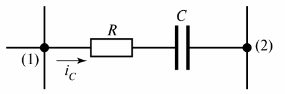
Rīsi. 2. Rezistīvi-kapacitatīvs atzars

Var sniegt citu atzara definīciju — tā ir ķēdes posms starp diviem blakus esošiem mezgliem (mezgli (1) un (2) 2. attēlā).

Ķēde Vai elektriskajā ķēdē ir slēgts ceļš. Ķēdi var slēgt ar jebkuriem zariem, ieskaitot nosacītos zarus, kuru pretestība ir vienāda ar bezgalību.

attēlā. 3 parādīta sazarota elektriskā ķēde, kas sastāv no trim atzariem.

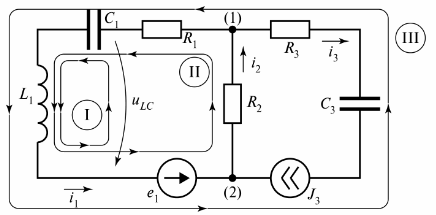
Rīsi. 3. Elektriskā ķēde ar divām ķēdēm

Diagrammā parādītas trīs ķēdes, un I ķēde ir slēgta ar bezgalīgas pretestības atzaru. Šī filiāle ir norādīta kā spriegums tiLC.

Att. shēmai. 3 iespējams sastādīt daudzas cilpas, kuras noslēdz reāli vai nosacīti atzari, bet elektriskā trokšņa aprēķināšanai tiek izmantots jēdziens «neatkarīgs cilpa». Neatkarīgo ķēdes cilpu skaits vienmēr ir iestatīts kā minimālais, kas nepieciešams aprēķinam.

Neatkarīgās ķēdes vienmēr ir slēgtas, bet zari, kuru pretestība nav vienāda ar bezgalību, un katra neatkarīgā ķēde ietver vismaz vienu atzaru, kas nav iekļauta citās ķēdēs. Sarežģītām elektriskām shēmām neatkarīgo ķēžu skaitu var noteikt, izmantojot shēmas shēmu.

Uz ķēdes shēmas tiek izsaukts nosacīts ķēdes attēlojums, kurā katrs atzars tiek aizstāts ar līnijas segmentu. Vienumi filiālēs netiek parādīti. Piemēram, Fig. 4 parāda atzaru ķēdi un tās diagrammu.

Rīsi. 4. Sazarotā elektriskā ķēde: a — shēma, b — shēma

Lai izveidotu diagrammas diagrammu, mezgli ir jāsavieno ar atzarojuma līnijām, nenorādot uz tiem elementus. Zari ir numurēti, un straumju virzieni uz tiem ir norādīti ar bultiņām. Pašam grafikam nav fiziskas nozīmes, taču to var izmantot, lai noteiktu neatkarīgo kontūru skaitu un veidu. Šim nolūkam tiek sagatavots "grafiskais koks".

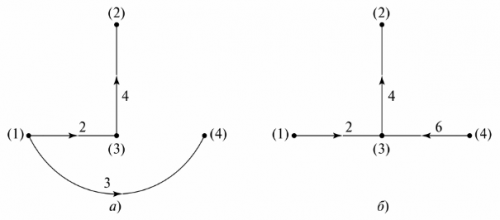
Grafiskais koks Tas attēlo shēmas grafiku, kuras mezgli ir savienoti ar zariem tā, lai neradītu slēgtu cilpu. Grafiskā koka attēlošanai var būt vairākas iespējas. attēlā. 5 parādītas divas iespējamās shēmas Fig. 4.

Rīsi. 5. Shēmas grafiskais koks

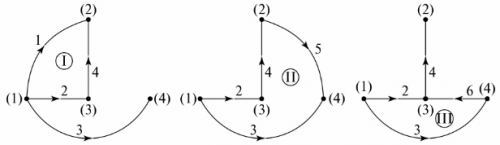
Grafu kokā trūkstošo zaru skaits ir vienāds ar ķēdes neatkarīgo cilpu skaitu. Piemērā tās ir trīs filiāles, trīs neatkarīgas cilpas. Neatkarīgo cilpu konfigurāciju var iegūt, secīgi savienojot grafu koka mezglus ar zariem, kas nav norādīti grafu kokā. Piemēram, grafika kokam attēlā. 5, un neatkarīgās kontūras ir parādītas attēlā. 6.

Rīsi. 6. Neatkarīgu kontūru noteikšana caur grafiku koku

Neatkarīgu ķēžu konfigurēšanas opcijas izvēle ķēdes aprēķināšanai tiek veikta ķēdes analīzes laikā. Jāizvēlas tādas kontūras, lai aprēķins būtu pēc iespējas vienkāršāks, t.i. atkarīgo vienādojumu skaits sistēmā ir minimāls.

Topoloģiskie vienādojumi nosaka attiecības starp spriegumiem un strāvām ķēdē, un vienādojumu skaits un veids nav atkarīgs no tā, kuri elementi ir iekļauti zaros. Topoloģiskie vienādojumi ietver vienādojumus, kas sastāv no saskaņā ar Kirhhofa likumiem.