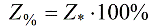Relatīvo vienību sistēma
Lai vienkāršotu aprēķinus, aprēķinot parametrus elektroenerģijas pārvades sistēmās, tiek izmantota relatīvo vienību sistēma. Šī metode ietver sistēmas vērtības pašreizējās vērtības izteikšanu kā bāzes (bāzes) vērtību, kas ņemta par vienību.
Tātad relatīvā vērtība tiek izteikta kā bāzes vērtības reizinātājs (strāva, spriegums, pretestība, jauda utt.) un nav atkarīga no sprieguma līmeņa, izteikta relatīvās vienībās. Angļu literatūrā relatīvās vienības tiek apzīmētas ar pu vai p.u. (no vienību sistēmas — relatīvo vienību sistēma).
Piemēram, viena veida transformatoriem sprieguma kritums, pretestība un zudumi atšķiras pēc absolūtās vērtības pie dažādiem pielietotajiem spriegumiem. Bet relatīvajos izmēros tie paliks aptuveni tādi paši. Kad aprēķins ir veikts, rezultāti tiek viegli konvertēti atpakaļ sistēmas vienībās (ampēros, voltos, omos, vatos utt.), jo sākotnēji ir zināmas bāzes vērtības, ar kurām tiek salīdzinātas pašreizējās vērtības.
Pārraidītās jaudas aprēķināšanai parasti ir ērtas relatīvās vienības, taču bieži gadās, ka motora ģeneratoru un transformatoru parametri tiek norādīti relatīvās vienībās, tāpēc katram inženierim ir jāzina relatīvo vienību jēdziens. Relatīvā vienību sistēmā tiek izmantotas jaudas, strāvas, sprieguma, pretestības, pielaides vienības. Jauda un spriegums ir neatkarīgi lielumi, ko nosaka reālu energosistēmu īpašības.
Visas sistēmas tīkla vērtības var izteikt kā atlasīto bāzes vērtību reizinājumus. Tātad, ja mēs runājam par jaudu, tad par bāzes vērtību var izvēlēties transformatora nominālo jaudu. Gadās, ka noteiktā brīdī iegūtā jauda relatīvās vērtības veidā ievērojami atvieglo aprēķinus. Sprieguma pamats ir kopnes nominālais spriegums utt.
Kopumā konteksts vienmēr ļauj saprast, par kādu relatīvo vērtību tiek runāts, un pat viena un tā paša simbola "pu" klātbūtne angļu literatūrā jūs nemulsinās.
Tātad visi sistēmas fizikālie lielumi tiek nosaukti. Bet, kad mēs tos tulkojam relatīvās vienībās (faktiski procentos), teorētisko aprēķinu būtība tiek vispārināta.
Kāda fiziskā lieluma relatīvā vērtība tiek saprasta kā tā saistība ar kādu bāzes vērtību, tas ir, ar vērtību, kas izvēlēta kā vienība konkrētam mērījumam. Relatīvā vērtība zemāk ir atzīmēta ar zvaigznīti.
Bieži vien aprēķinos tiek ņemtas šādas pamatvērtības: pamata pretestība, pamata strāva, pamata spriegums un pamata jauda.
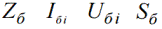
Apakšraksts «b» norāda, ka tā ir bāzes vērtība.
Tad relatīvās mērvienības tiks sauktas par relatīvajām pamata:
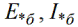
Zvaigznīte norāda relatīvo vērtību, burts «b» - bāzi. EML ir relatīvi fundamentāls, strāva ir relatīvi fundamentāla utt. Un relatīvās bāzes vienības tiks noteiktas ar šādām izteiksmēm:
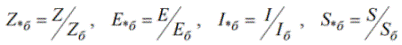
Piemēram, lai izmērītu leņķiskos ātrumus, leņķiskais sinhronais ātrums tiek pieņemts kā vienība, un tāpēc sinhronais leņķiskais ātrums būs vienāds ar pamata leņķisko ātrumu.
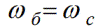
Tad patvaļīgu leņķisko ātrumu var izteikt relatīvās vienībās:
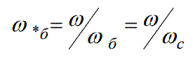
Attiecīgi plūsmas savienojumam un induktivitātei par pamatattiecībām var uzskatīt šādas attiecības:
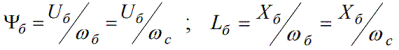
Šeit galvenā plūsmas saite ir plūsmas saite, kas izraisa galveno spriegumu pie galvenā leņķiskā ātruma.
Tātad, ja par pamatu tiek ņemts sinhronais leņķiskais ātrums, tad:
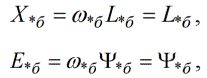
relatīvajās vienībās emf ir vienāds ar plūsmu un induktīvā pretestība ir vienāda ar induktivitāti. Tas ir tāpēc, ka bāzes vienības ir izvēlētas atbilstoši.
Pēc tam apsveriet fāzes spriegumu relatīvajās un pamatvienībās:
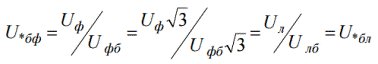
Ir viegli redzēt, ka fāzes spriegums relatīvajās pamatvienībās ir vienāds ar lineāro relatīvo pamatspriegumu. Līdzīgi, sprieguma amplitūdas vērtība relatīvajās vienībās izrādās vienāda ar efektīvo:
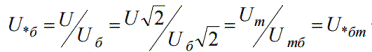
No šīm atkarībām ir redzams, ka relatīvās vienībās pat trīs fāžu jauda un vienas fāzes jauda ir vienāda, un ģeneratora ierosmes strāvas, plūsmas un emf - arī izrādās vienādas.
Šeit ir svarīgi atzīmēt, ka katram ķēdes elementam relatīvā pretestība būs vienāda ar relatīvo sprieguma kritumu ķēdei piegādātās nominālās jaudas apstākļos.
Aprēķinot īssavienojuma strāvas, tiek izmantoti četri galvenie parametri: strāva, spriegums, pretestība un jauda. Sprieguma un jaudas pamatvērtības tiek uzskatītas par neatkarīgām, un caur tām tiek izteikta pamata pretestība un strāva. No trīsfāzu tīkla jaudas vienādojuma — strāva, tad Oma likums — pretestība:
Tā kā bāzes vērtību var izvēlēties patvaļīgi, vienam un tam pašam fiziskajam daudzumam, kas izteikts relatīvās vienībās, var būt dažādas skaitliskās vērtības. Tāpēc ģeneratoru, motoru, transformatoru relatīvās pretestības tiek iestatītas relatīvās vienībās, ievadot relatīvās nominālās vienības. Sn — nominālā jauda. Un — nominālais spriegums. Relatīvās nominālvērtības raksta ar indeksu «n»:
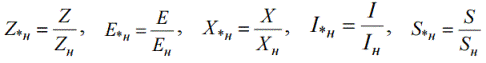
Lai atrastu nominālās pretestības un strāvas, tiek izmantotas standarta formulas:
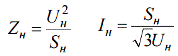
Lai noteiktu attiecības starp relatīvajām vienībām un nosauktajiem lielumiem, vispirms izsakām attiecības starp relatīvo bāzi un bāzes daudzumiem:
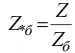
Uzrakstīsim bāzes pretestību jaudas un aizstājēja izteiksmē:
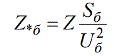
Tātad jūs varat pārvērst norādīto vērtību relatīvā bāzes vērtībā.
Un līdzīgā veidā jūs varat izveidot attiecības starp relatīvajām nominālvienībām un lietvārdiem:
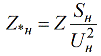
Lai aprēķinātu pretestību nosauktajās vienībās ar zināmām relatīvajām nominālvērtībām, izmantojiet šādu formulu:
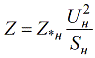
Attiecību starp relatīvajām nominālajām vienībām un relatīvajām bāzes vienībām nosaka pēc šādas formulas:
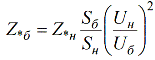
Izmantojot šo formulu, relatīvās nominālās vienības var pārvērst relatīvās bāzes vienībās.
Energosistēmās, lai ierobežotu īssavienojuma strāvas, iestatīt pašreizējie ierobežotie reaktori, faktiski — lineārie induktori. Tie saņem nominālo spriegumu un strāvu, bet ne jaudu.
Atsaucoties uz
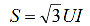
un pārveidojot iepriekš minētās izteiksmes relatīvajai nominālajai un relatīvajai bāzes pretestībai, mēs iegūstam:
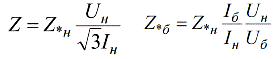
Relatīvās vērtības var izteikt procentos:
