Nesazarotas un sazarotas lineāras elektriskās ķēdes ar vienu padevi
 Ja liels skaits pasīvo elementu kopā ar avotu e. utt. c) veido elektrisko ķēdi, to savstarpējo savienojumu var veikt dažādos veidos. Šādiem savienojumiem ir šādas tipiskas shēmas.
Ja liels skaits pasīvo elementu kopā ar avotu e. utt. c) veido elektrisko ķēdi, to savstarpējo savienojumu var veikt dažādos veidos. Šādiem savienojumiem ir šādas tipiskas shēmas.
Elementu seriālais savienojums Šis ir vienkāršākais savienojums. Ar šo savienojumu visos ķēdes elementos plūst viena un tā pati strāva. Saskaņā ar šo shēmu var savienot vai nu visus ķēdes pasīvos elementus, un tad ķēde būs viena ķēde nesazarota (1. att., a), vai arī var būt tikai daļa no daudzķēžu ķēdes elementiem. savienots.
Ja virknē ir savienoti n elementi, kuros plūst viena un tā pati strāva I, tad spriegums ķēdes spailēs būs vienāds ar sprieguma kritumu summu n virknē savienotos elementos, t.i.
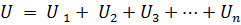
vai:
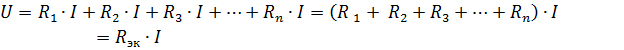
kur Rek ir līdzvērtīgā ķēdes pretestība.
Tāpēc virknē savienoto pasīvo elementu ekvivalentā pretestība ir vienāda ar šo elementu pretestību summu... Elektriskā shēma (att.1, a) var uzrādīt līdzvērtīgu ķēdi (1. att., b), kas sastāv no viena elementa ar līdzvērtīgu pretestību Rek
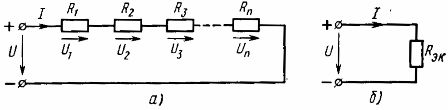
Rīsi. 1. Lineāro elementu seriālā savienojuma shēma (a) un tai līdzvērtīgā shēma (b)
Aprēķinot ķēdi ar virknē savienotiem elementiem ar noteiktu strāvas avota spriegumu un elementu pretestībām, strāvu ķēdē aprēķina saskaņā ar Ohma likumu:
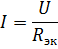
Sprieguma kritums kth elementā
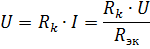
ir atkarīgs ne tikai no šī elementa pretestības, bet arī no līdzvērtīgās pretestības Rek, tas ir, no citu ķēdes elementu pretestības. Tas ir būtisks elementu sērijveida savienojuma trūkums. Ierobežotajā gadījumā, kad jebkura ķēdes elementa pretestība kļūst vienāda ar bezgalību (atvērta ķēde), strāva visos ķēdes elementos kļūst par nulli.
Tā kā, savienojot virknē, strāva visos ķēdes elementos ir vienāda, elementu sprieguma krituma attiecība ir vienāda ar šo elementu pretestību attiecību:
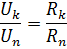
Elementu paralēlais savienojums - tas ir savienojums, kurā visiem ķēdes elementiem tiek pielikts vienāds spriegums. Saskaņā ar paralēlā savienojuma shēmu var savienot vai nu visus ķēdes pasīvos elementus (2. att., a), vai tikai daļu no tiem. Katrs paralēli savienotais elements veido atsevišķu atzaru. Tāpēc ķēde ar paralēlu elementu savienojumu, kas parādīts attēlā. 2, a, lai gan tā ir vienkārša ķēde (jo tajā ir tikai divi mezgli), tā vienlaikus ir sazarota.
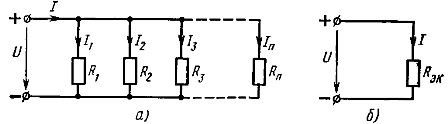
Rīsi. 2. Lineāro elementu paralēlā savienojuma shēma (a) un tai līdzvērtīga shēma (b)
Katrā paralēlajā zarā strāva
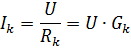
kur Gk ir k-tā zara vadītspēja.
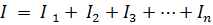
vai
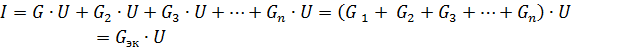
kur Gec ir līdzvērtīga ķēdes vadītspēja.
Tāpēc, paralēli savienojot pasīvos elementus, to ekvivalentā vadītspēja ir vienāda ar šo elementu vadītspēju summu... Ekvivalentā vadītspēja vienmēr ir lielāka par jebkuras paralēlo zaru daļas vadītspēju. Ekvivalentā vadītspēja GEK atbilst ekvivalentajai pretestībai Rek = 1 / Gek.
Pēc tam ekvivalentā ķēde, kas parādīta attēlā. 2, a, būs tāda forma, kas parādīta 2. attēlā. 2, b. Strāvu ķēdes nesazarotajā daļā ar elementu paralēlu savienojumu var noteikt no šīs ķēdes saskaņā ar Oma likumu:
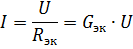
Tāpēc, ja barošanas spriegums ir nemainīgs, tad, palielinoties paralēli savienoto elementu skaitam (kas noved pie ekvivalentās vadītspējas palielināšanās), strāva ķēdes nesazarotajā daļā (barošanas strāva) palielinās.
No formulas
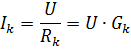
redzams, ka strāva katrā atzarā ir atkarīga tikai no šī zara vadītspējas un nav atkarīga no citu atzaru vadītspējas. Paralēlo zaru režīmu neatkarība viens no otra ir svarīga pasīvo elementu paralēlā savienojuma priekšrocība. Rūpnieciskajās iekārtās vairumā gadījumu tiek izmantots elektrisko uztvērēju paralēlais savienojums. Acīmredzamākais piemērs ir elektrisko lampu iekļaušana apgaismojumā.
Tā kā paralēlā savienojumā visiem elementiem tiek pielikts vienāds spriegums un strāva katrā atzarā ir proporcionāla šī atzara vadītspējai, tad paralēlajos zaros esošo strāvu attiecība ir vienāda ar šo zaru vadītspēju attiecību jeb apgriezti proporcionāla pret to pretestības attiecību:
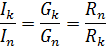
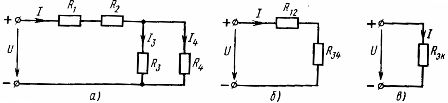
Jaukts elementu savienojums ir virknes un paralēlu savienojumu kombinācija. Šādai ķēdei var būt atšķirīgs mezglu un zaru skaits. Jaukta savienojuma piemērs ir parādīts diagrammā (3. att., a)
Rīsi. 3. Lineāro elementu jauktā savienojuma shēma (a) un tai ekvivalentās shēmas (b, c).
Lai aprēķinātu šādu ķēdi, ir secīgi jānosaka ekvivalentās pretestības tām ķēdes daļām, kuras ir tikai virknes vai tikai paralēlas pieslēgums. Aplūkotajā shēmā ir elementu virknes savienojums ar pretestībām R1 un R2 un elementu paralēlais savienojums ar pretestībām R3 un R4. Izmantojot iepriekš iegūtās attiecības starp ķēdes elementu parametriem ar to virknes un paralēlo savienojumu, reālo elektrisko ķēdi var secīgi aizstāt ar līdzvērtīgām shēmām.
Sērijveidā savienoto elementu ekvivalentā pretestība
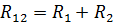
Paralēli savienoto elementu R3 un R4 ekvivalentā pretestība
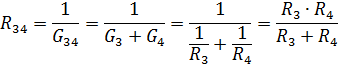
Līdzvērtīga ķēde ar elementu R12 un R34 pretestībām ir parādīta attēlā. 3, b. Šim R12 un R34 sērijas savienojumam līdzvērtīga pretestība ir
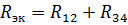
un atbilstošā ekvivalentā ķēde ir parādīta attēlā. 2, b. Atradīsim strāvu šajā ķēdē:
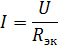
Tā ir barošanas strāva un strāva reālās ķēdes elementos R1 un R2.Lai aprēķinātu strāvas I3 un I4, nosakiet spriegumu ķēdes posmā ar pretestību R34 (3. att., b):
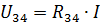
Tad strāvas I3 un I4 var atrast saskaņā ar Ohma likumu:
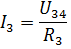
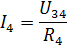
Līdzīgā veidā jūs varat aprēķināt vairākas citas elektriskās ķēdes ar jauktu pasīvo elementu savienojumu.
Sarežģītām shēmām ar lielu skaitu ķēžu un avotu e. utt. c) šādu līdzvērtīgu pārveidošanu ne vienmēr var veikt. Tos aprēķina ar citām metodēm.