Nelineāras elektriskās ķēdes
Nelineāro elementu mērķis elektriskajās ķēdēs
V elektriskās ķēdes var ietvert pasīvos elementus, elektriskā pretestība kas būtībā ir atkarīgs no strāvas vai sprieguma, kā rezultātā strāva nav tieši proporcionāla spriegumam. Šādus elementus un elektriskās ķēdes, kurās tie nonāk, sauc par nelineāriem elementiem.
Nelineārie elementi piešķir elektriskajām ķēdēm tādas īpašības, kas nav sasniedzamas lineārajās ķēdēs (sprieguma vai strāvas stabilizācija, līdzstrāvas pastiprināšana utt.). Tie ir nekontrolējami un vadāmi... Pirmais — bipolārais — paredzēts darbam bez kontroles faktora ietekmes uz tiem (pusvadītāju termistori un diodes), bet otrs — daudzpolārs — tiek izmantots, kad uz tiem iedarbojas kontroles faktors (tranzistori). un tiristori).
Nelineāro elementu strāvas-sprieguma raksturlielumi
Nelineāro elementu elektriskās īpašības ir strāvas-sprieguma raksturlielumu I (U) eksperimentāli iegūti grafiki, kas parāda strāvas atkarību no sprieguma, kuriem dažkārt tiek veidota aptuvena, aprēķiniem ērta empīriskā formula.
Nekontrolētiem nelineāriem elementiem ir viens strāvas-sprieguma raksturlielums, un kontrolētiem nelineāriem elementiem ir šādu raksturlielumu saime, kuru parametrs ir kontrolējošais faktors.
Lineārajiem elementiem ir nemainīga elektriskā pretestība, tāpēc to strāvas-sprieguma raksturlielums ir taisna līnija, kas iet caur izcelsmi (1. att., a).
Nelineāro strāvas-sprieguma raksturlielumiem ir atšķirīga forma un tie ir sadalīti simetriskajos un asimetriskos attiecībā pret koordinātu asīm (1. att., b, c).
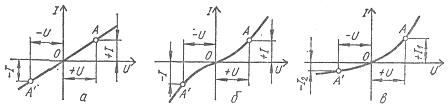
Rīsi. 1. Pasīvo elementu strāvas-sprieguma raksturlielumi: a — lineāri, b — nelineāri simetriskie, c — nelineāri asimetriskie
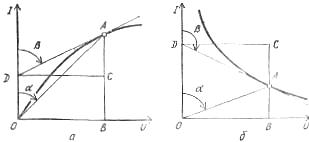
Rīsi. 2. Grafiki nelineāro elementu statiskās pretestības noteikšanai diferenciālās pretestības noteikšanai strāvas-sprieguma raksturlielumu sadaļās: a — pieaug, b — krīt.
Nelineāriem elementiem ar simetrisku strāvas-sprieguma raksturlielumu vai simetriskiem elementiem sprieguma virziena maiņa neizraisa strāvas vērtības izmaiņas (1. att., b), bet nelineāriem elementiem ar asimetrisku spriegumu. -strāvas raksturlielums jeb asimetriskiem elementiem, ar vienu un to pašu pretējos virzienos virzīta sprieguma absolūto vērtību, strāvas ir dažādas (1. att., c). Tāpēc līdzstrāvas un maiņstrāvas ķēdēs tiek izmantoti nelineāri simetriski elementi, bet maiņstrāvas ķēdēs parasti tiek izmantoti nelineāri nelīdzsvaroti elementi, lai pārveidotu maiņstrāvu līdzstrāvā.
Nelineāro elementu raksturojums
Katram nelineārajam elementam tiek izdalīta statiskā pretestība, kas atbilst konkrētam strāvas-sprieguma raksturlīknes punktam, piemēram, punkts A:
Rst = U / I = muOB / miBA = mr tgα
un diferenciālā pretestība, kas paredzēta. to pašu punktu A nosaka pēc formulas:
Rdiff = dU / dI = muDC / miCA = mr tgβ,
kur mi, mi, sir — attiecīgi spriegumu, strāvu un pretestību skala.
Statiskā pretestība raksturo nelineāra elementa īpašības pastāvīgās strāvas režīmā, bet diferenciālā pretestība — nelielām strāvas novirzēm no līdzsvara stāvokļa vērtības. Abi mainās, pārejot no viena punkta, un strāvas sprieguma raksturlielums uz otru, pirmais vienmēr ir pozitīvs, bet otrais mainīgais: raksturlīknes augošajā daļā strāvas spriegums ir pozitīvs, bet krītošajā - negatīvs.
Nelineāros elementus raksturo arī abpusējas vērtības: statiskā vadītspēja Gst un diferenciālā vadītspēja Gdažādi vai bezizmēra parametri —
relatīvā pretestība:
Kr = — (R starpība / Rst)
vai relatīvā vadītspēja:
Kg = — (G starpība / Gst)
Lineārajiem elementiem parametri Kr un Kilograms ir vienādi ar vienu, un nelineāriem elementiem tie atšķiras no tā, un jo vairāk tie atšķiras no viena, jo vairāk izpaužas elektriskās ķēdes nelinearitāte.
 Nelineāro elektrisko ķēžu aprēķins
Nelineāro elektrisko ķēžu aprēķins
Nelineārās elektriskās ķēdes tiek aprēķinātas grafiski un analītiski, pamatojoties uz Kirhofa likumi un maiņstrāvas ķēžu atsevišķu elementu volt-ampēru raksturlielumi maiņstrāvas pārvēršanai līdzstrāvā.
Grafiski aprēķinot elektrisko ķēdi ar diviem sērijveidā savienotiem nelineāriem rezistoriem R1 un R2 ar strāvas-sprieguma raksturlielumiem Iz (U1) un Iz (U2), izveidojiet strāvas-sprieguma raksturlielumu visai ķēdei Iz (U), kur U = U1 + U2, kuru punktu abscises atrod, summējot nelineāro rezistoru strāvas-sprieguma raksturlielumu punktu abscises ar vienādām ordinātām (3. att., a, b).
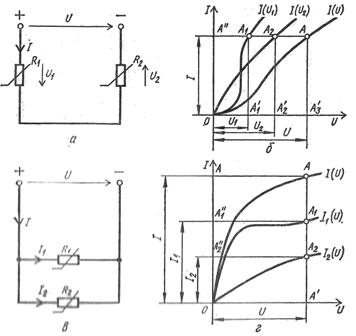
Rīsi. 3. Nelineāro elektrisko ķēžu diagrammas un raksturlielumi: a — nelineāro rezistoru virknes savienojuma shēma, b — atsevišķu elementu un virknes ķēdes voltampēru raksturlielumi, c — nelineāro rezistoru paralēlā savienojuma shēma, d — atsevišķu elementu un paralēlās ķēdes volt-ampēru raksturlielumi.
Šīs līknes klātbūtne ļauj spriegumam U atrast strāvu Az, kā arī spriegumu U1 un U2 rezistoru spailēs.
Tādā pašā veidā tiek veikts elektriskās ķēdes aprēķins ar diviem paralēli savienotiem rezistoriem. R1 un R2 ar strāvas-sprieguma raksturlielumiem I1 (U) un Az2 (U), kuriem tika uzbūvēts visas ķēdes strāvas-sprieguma raksturlielums Az(U), kur Az = I1+I2, uz kura, izmantojot doto spriegumu U, atrodiet strāvas Az , I1, I2 (oriz. 3, c, d).
Analītiskā metode nelineāro elektrisko ķēžu aprēķināšanai ir balstīta uz nelineāro elementu sprieguma raksturlielumu uzrādīšanu, izmantojot atbilstošo matemātisko funkciju vienādojumus, kas ļauj sastādīt nepieciešamos elektrisko ķēžu stāvokļu vienādojumus. .Tā kā šādu nelineāru vienādojumu risināšana bieži rada ievērojamas grūtības, analītiskā metode nelineāro ķēžu aprēķināšanai ir ērta, ja var iztaisnot nelineāro elementu strāvas-sprieguma raksturlielumu darbības sadaļas. Tas ļauj aprakstīt ķēdes elektrisko stāvokli ar lineāriem vienādojumiem, kas nerada grūtības to risināšanā.
Elektrotehnikas pamati:
Par potenciālu starpību, elektromotora spēku un spriegumu
Elektriskā strāva šķidrumos un gāzēs
Magnētisms un elektromagnētisms
Par magnētisko lauku, solenoīdiem un elektromagnētiem
Pašindukcija un savstarpēja indukcija
Elektriskais lauks, elektrostatiskā indukcija, kapacitāte un kondensatori
Kas ir maiņstrāva un kā tā atšķiras no līdzstrāvas

