Elektromagnētiskās vibrācijas — bez slāpēšanas un piespiedu vibrācijām
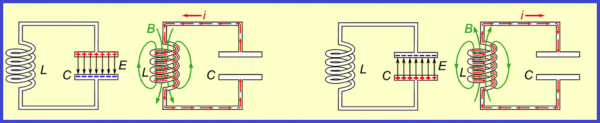
Elektromagnētiskās vibrācijas ķēdē, kas sastāv no induktora un kondensatora, rodas periodiskas elektriskās enerģijas pārvēršanas dēļ magnētiskajā enerģijā un otrādi. Šajā gadījumā periodiski mainās elektriskais lādiņš uz kondensatora plāksnēm un strāvas stiprums caur spoli.

Elektromagnētiskās vibrācijas ir brīvas un piespiedu kārtā. Brīvās svārstības, kā likums, tiek slāpētas nulles cilpas pretestības dēļ, un piespiedu svārstības parasti ir pašsvārstības.
Iegūt vibrācijas ķēdē brīvas svārstības, mums vispirms ir jāizved šī sistēma no līdzsvara: informē kondensatoru ar sākotnējo lādiņu q0 vai kaut kādā veidā iniciē strāvas impulsu I0 caur spoli.
Tas kalpos kā sava veida impulss un ķēdē notiks brīvas elektromagnētiskās svārstības - sāksies mainīgas kondensatora uzlādes un izlādes process caur induktīvo spoli un attiecīgi spoles magnētiskā lauka mainīgais kāpums un kritums.
Svārstības, kuras ķēdē uztur ārējs mainīgs elektromotora spēks, sauc par piespiedu svārstībām. Tātad, kā jūs jau sapratāt, vienkāršākās svārstību sistēmas piemērs, kurā var novērot brīvas elektromagnētiskās svārstības, ir svārstību ķēde, kas sastāv no kondensatora ar elektrisko kapacitāti C un spoles ar induktivitāti L.
Reālā svārstību ķēdē periodiski atkārtojas kondensatora uzlādes process, bet svārstības ātri izzūd, jo enerģija tiek izkliedēta galvenokārt uz spoles stieples aktīvās pretestības R.
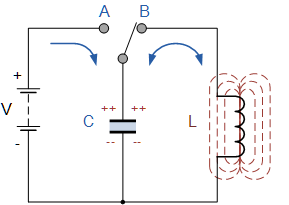
Apsveriet ķēdi ar ideālu svārstību ķēdi. Vispirms uzlādēsim kondensatoru no akumulatora — piešķirsim tam sākotnējo uzlādi q0, tas ir, piepildīsim kondensatoru ar enerģiju. Tā būs kondensatora We maksimālā enerģija.
Nākamais solis ir atvienot kondensatoru no akumulatora un savienot to paralēli induktors. Šajā brīdī kondensators sāks izlādēties, un spoles ķēdē parādīsies pieaugoša strāva. Jo ilgāk kondensators izlādējas, jo vairāk lādiņa no tā pakāpeniski nonāk spolē, jo lielāka kļūst strāva spolē, tādējādi spole uzglabā enerģiju magnētiskā lauka veidā.
Šis process nenotiek uzreiz, bet pakāpeniski, jo spolei ir induktivitāte, kas nozīmē, ka notiek pašindukcijas parādība, kas sastāv no tā, ka spole vienalga pretojas strāvas palielinājumam. Kādā brīdī spoles magnētiskā lauka enerģija sasniedz maksimālo iespējamo vērtību Wm (atkarībā no tā, cik liels lādiņš sākotnēji tika pārnests uz kondensatoru un kāda ir ķēdes pretestība).
Arī pašindukcijas fenomena dēļ strāva caur spoli tiek uzturēta tajā pašā virzienā, taču tās lielums samazinās un elektriskais lādiņš galu galā atkal uzkrājas kondensatorā. Tādā veidā kondensators tiek uzlādēts. Tā plāksnēm tagad ir pretējas uzlādes zīmes nekā eksperimenta sākumā, kad mēs pievienojām kondensatoru akumulatoram.
Kondensatora enerģija ir sasniegusi maksimālo iespējamo vērtību šai ķēdei. Strāva ķēdē ir apstājusies. Tagad process sāk iet pretējā virzienā.Un tas turpināsies atkal un atkal, tas ir, būs brīvas elektromagnētiskās svārstības.
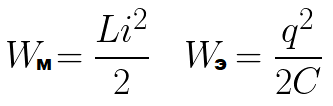
Ja ķēdes R aktīvā pretestība ir vienāda ar nulli, tad spriegums uz kondensatora plāksnēm un strāva caur spoli mainīsies bezgalīgi saskaņā ar harmonikas likumu - kosinusu vai sinusu. To sauc par harmonisko vibrāciju. Uzlāde uz kondensatora plāksnēm arī mainītos saskaņā ar harmonikas likumu.
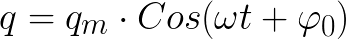
Ideālā ciklā nav nekādu zaudējumu. Un ja tā būtu, tad brīvo svārstību periods ķēdē būtu atkarīgs tikai no kondensatora kapacitātes C vērtības un spoles induktivitātes L. Šo periodu var atrast (ideālai cilpai ar R = 0), izmantojot Tomsona formulu:
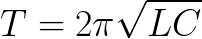
Atbilstošā frekvence un cikla frekvence tiek atrasta ideālai bezzudumu ķēdei, izmantojot šādas formulas:
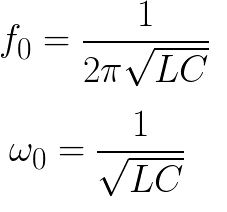
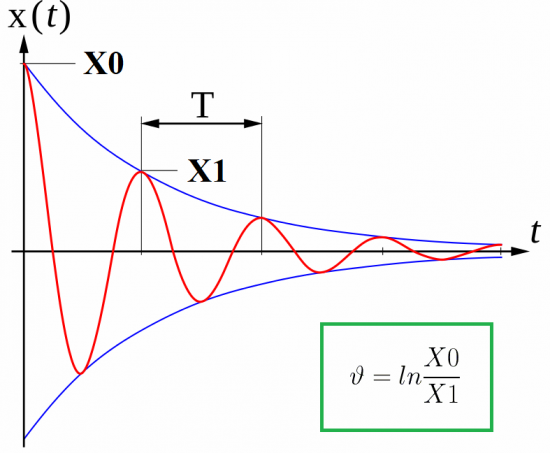
Taču ideālas shēmas neeksistē, un elektromagnētiskās svārstības tiek slāpētas vadu sildīšanas radīto zudumu dēļ. Atkarībā no ķēdes pretestības R vērtības katrs nākamais maksimālais kondensatora spriegums būs zemāks par iepriekšējo.
Saistībā ar šo parādību fizikā tiek ieviests tāds parametrs kā svārstību logaritmiskais samazinājums vai slāpēšanas samazinājums. To var atrast kā divu secīgu (vienas zīmes) svārstību maksimumu attiecības naturālo logaritmu:
Logaritmisko svārstību samazinājums ir saistīts ar ideālo svārstību periodu ar sekojošu sakarību, kur var ieviest papildu parametru, t.s. Amortizācijas koeficients:
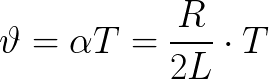
Slāpēšana ietekmē brīvo vibrāciju biežumu. Tāpēc formula brīvo slāpēto svārstību frekvences atrašanai reālā svārstību ķēdē atšķiras no ideālas ķēdes formulas (tiek ņemts vērā slāpēšanas koeficients):
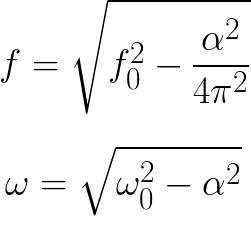
Lai ķēdē radītu svārstības izslēgts, ir nepieciešams šos zaudējumus papildināt un kompensēt katru pusperiodu. Tas tiek panākts nepārtrauktu svārstību ģeneratoros, kur ārējais EML avots kompensē siltuma zudumus ar savu enerģiju. Šādu svārstību sistēmu ar ārēju EML avotu sauc par pašoscilējošu.