Kas ir iekšējā pretestība

Pieņemsim, ka ir vienkārša elektriskā slēgta ķēde, kas ietver strāvas avotu, piemēram, ģeneratoru, galvanisko elementu vai akumulatoru, un rezistoru ar pretestību R. Tā kā strāva ķēdē nekur netiek pārtraukta, tā plūst arī avota iekšpusē.

Šādā situācijā mēs varam teikt, ka katram avotam ir kāda iekšējā pretestība, kas neļauj strāvai plūst. Šī iekšējā pretestība raksturo strāvas avotu un tiek apzīmēta ar burtu r. Priekš galvaniskais elements vai akumulators, iekšējā pretestība ir elektrolīta šķīduma un elektrodu pretestība, ģeneratoram - statora tinumu pretestība utt.

Tādējādi strāvas avotu raksturo gan EML lielums, gan tā iekšējās pretestības r vērtība — abi raksturlielumi norāda uz avota kvalitāti.

Augstsprieguma elektrostatiskajiem ģeneratoriem (piemēram, Van de Graaf ģeneratoram vai Wimshurst ģeneratoram), piemēram, ir milzīgs EML, ko mēra miljonos voltu, savukārt to iekšējā pretestība tiek mērīta simtos megaomu, tāpēc tie nav piemēroti iegūšanai. lielas strāvas.

Gluži pretēji, galvaniskajām šūnām (piemēram, akumulatoriem) EML ir aptuveni 1 volts, lai gan to iekšējā pretestība ir daļa vai ne vairāk kā desmit omi, un tāpēc var iegūt vienību un desmitiem ampēru strāvas. no galvaniskajiem elementiem.

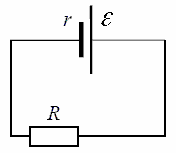
Šī diagramma parāda reālu avotu ar pievienotu slodzi. Tie ir definēti šeit EML avots, tā iekšējā pretestība, kā arī slodzes pretestība. Saskaņā ar Oma likums slēgtai ķēdei, strāva šajā ķēdē būs vienāda ar:

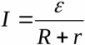
Tā kā ārējās ķēdes sadaļa ir viendabīga, tad no Oma likuma var atrast spriegumu pāri slodzei:

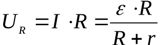
Izsakot slodzes pretestību no pirmā vienādojuma un aizstājot tās vērtību otrajā vienādojumā, iegūstam slodzes sprieguma atkarību no strāvas slēgtā ķēdē:

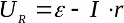
Slēgtā kontūrā EMF ir vienāds ar ārējo ķēdes elementu un paša avota iekšējās pretestības sprieguma krituma summu. Slodzes sprieguma atkarība no slodzes strāvas ideālā gadījumā ir lineāra.

Grafiks to parāda, bet eksperimentālie dati par reālu rezistoru (krusti pie grafika) vienmēr atšķiras no ideālajiem:

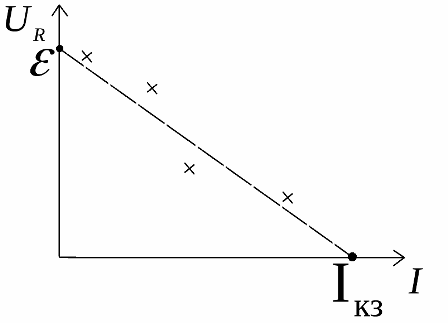
Eksperimenti un loģika parāda, ka pie nulles slodzes strāvas ārējās ķēdes spriegums ir vienāds ar avota emf un pie nulles slodzes sprieguma ķēdes strāva ir īssavienojuma strāva… Šī reālo ķēžu īpašība palīdz eksperimentāli atrast reālo avotu EML un iekšējo pretestību.

Iekšējās pretestības eksperimentāla noteikšana

Lai eksperimentāli noteiktu šos raksturlielumus, tiek izveidots grafiks par slodzes sprieguma atkarību no strāvas lieluma, pēc kura to ekstrapolē līdz krustošanās punktam ar asīm.

Grafika krustošanās punktā ar sprieguma mugurkaulu ir avota emf vērtība, bet krustošanās punktā ar strāvas asi ir īssavienojuma strāvas vērtība. Rezultātā iekšējo pretestību nosaka pēc formulas:

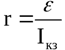
Avota izstrādātā lietderīgā jauda tiek sadalīta pa slodzi. Šīs jaudas atkarības no slodzes pretestības grafiks ir parādīts attēlā. Šī līkne sākas no koordinātu asu krustpunkta nulles punktā, pēc tam palielinās līdz maksimālajai jaudas vērtībai, pēc tam nokrītas līdz nullei ar slodzes pretestību, kas vienāda ar bezgalību.

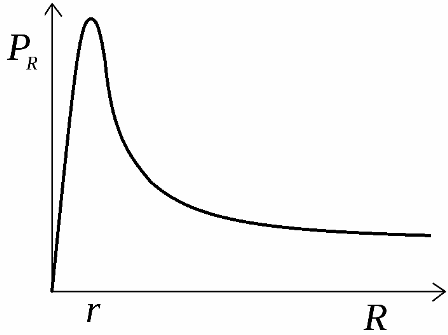
Lai atrastu maksimālo slodzes pretestību, pie kuras tiks attīstīta teorētiskā maksimālā jauda ar doto avotu, tiek ņemts jaudas formulas atvasinājums attiecībā pret R un iestatīts uz nulli. Maksimālā jauda tiks attīstīta, ja ārējā ķēdes pretestība ir vienāda ar iekšējo avota pretestību:

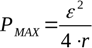
Šis nosacījums par maksimālo jaudu pie R = r ļauj eksperimentāli atrast avota iekšējo pretestību, attēlojot slodzes atbrīvoto jaudu pret slodzes pretestības vērtību.Faktiskās, nevis teorētiskās slodzes pretestības atrašana, kas nodrošina maksimālo jaudu, nosaka faktisko barošanas avota iekšējo pretestību.

Strāvas avota efektivitāte norāda slodzei sadalītās maksimālās jaudas attiecību pret kopējo jaudu, kas pašlaik tiek izstrādāta

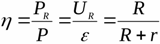
Ir skaidrs, ka, ja avots attīsta tādu jaudu, ka pie slodzes tiek iegūta maksimālā iespējamā jauda konkrētam avotam, tad avota efektivitāte būs vienāda ar 50%.