Aktīvā pretestība un induktors maiņstrāvas ķēdē

Ņemot vērā maiņstrāvas ķēdi, kurā ir tikai induktīva pretestība (skatiet rakstu "Induktors maiņstrāvas ķēdē"), mēs pieņēmām, ka šīs ķēdes aktīvā pretestība ir nulle.

Faktiski gan pašam spoles vadam, gan savienojošajiem vadiem ir neliela, bet aktīva pretestība, tāpēc ķēde neizbēgami patērē strāvas avota enerģiju.

Tāpēc, nosakot ārējās ķēdes kopējo pretestību, ir jāpievieno tās reaktīvā un aktīvā pretestība. Bet nav iespējams pievienot šīs divas pretestības, kurām ir atšķirīgs raksturs.

Šajā gadījumā ķēdes pretestība maiņstrāvai tiek noteikta ar ģeometrisku pievienošanu.

Tiek izveidots taisnleņķa trijstūris (skat. 1. attēlu), kura viena puse ir induktīvās pretestības vērtība, bet otra puse ir aktīvās pretestības vērtība. Vēlamo ķēdes pretestību nosaka trijstūra trešā mala.

1. attēls. Induktīvo un aktīvo pretestību saturošas ķēdes pretestības noteikšana

Ķēdes pretestība ir apzīmēta ar latīņu burtu Z, un to mēra omos. No konstrukcijas var redzēt, ka kopējā pretestība vienmēr ir lielāka par induktīvo un aktīvo pretestību atsevišķi.

Kopējās ķēdes pretestības algebriskā izteiksme ir:

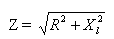
kur Z — kopējā pretestība, R — aktīvā pretestība, XL — ķēdes induktīvā pretestība.

Tāpēc ķēdes kopējā pretestība maiņstrāvai, kas sastāv no aktīvās un induktīvās pretestības, ir vienāda ar kvadrātsakni no šīs ķēdes aktīvās un induktīvās pretestības kvadrātu summas.

Oma likums jo šādu ķēdi izsaka ar formulu I = U / Z, kur Z ir ķēdes kopējā pretestība.

Tagad analizēsim, kāds būs spriegums, ja ķēdei papildus un un fāzes nobīdei starp strāvu un induktivitāti ir arī salīdzinoši liela aktīvā pretestība. Praksē šāda ķēde var būt, piemēram, ķēde, kurā ir dzelzs serdeņa induktors, kas apvilkts ar plānu stiepli (augstfrekvences droseļvārsts).

Šajā gadījumā fāzes nobīde starp strāvu un spriegumu vairs nebūs ceturtdaļa perioda (kā tas bija ķēdē ar tikai induktīvo pretestību), bet daudz mazāka; un jo lielāka pretestība, jo mazāka būs fāzes nobīde.

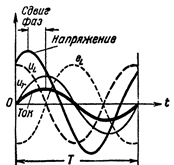
2. attēls. Strāva un spriegums ķēdē, kas satur R un L.

Tagad viņa pati Pašindukcijas EMF nav pretfāzē ar strāvas avota spriegumu, jo tas ir nobīdīts attiecībā pret spriegumu nevis par pusperiodu, bet mazāk.Turklāt strāvas avota radītais spriegums spoles spailēs nav vienāds ar pašindukcijas emf, bet ir lielāks par to par sprieguma krituma lielumu spoles vada aktīvajā pretestībā. Citiem vārdiem sakot, spriegums spolē sastāv no diviem komponentiem:

• tiL- sprieguma reaktīvā sastāvdaļa, kas līdzsvaro pašindukcijas EML efektu,

• tiR- sprieguma aktīvā sastāvdaļa, kas pārvarēs ķēdes aktīvo pretestību.

Ja virknē ar spoli savienosim lielu aktīvo pretestību, fāzes nobīde samazināsies tik ļoti, ka strāvas sinusoidālais vilnis gandrīz sasniegs sprieguma sinusoidālo vilni un fāžu atšķirība starp tām būs tikko manāma. termina amplitūda un būs lielāka par termina amplitūdu.

Tāpat jūs varat samazināt fāzes nobīdi un pat pilnībā samazināt to līdz nullei, ja kaut kādā veidā samazina ģeneratora frekvenci. Frekvences samazināšanās rezultātā samazināsies pašindukcijas EMF un līdz ar to samazināsies fāzes nobīde starp strāvu un tās izraisīto spriegumu ķēdē.

Maiņstrāvas ķēdes jauda, ​​kurā ir induktors

Maiņstrāvas ķēde, kurā ir spole, nepatērē strāvas avota enerģiju un ka ķēdē notiek enerģijas apmaiņas process starp ģeneratoru un ķēdi.

Tagad analizēsim, kā būs ar jaudu, ko patērē šāda shēma.

Maiņstrāvas ķēdē patērētā jauda ir vienāda ar strāvas un sprieguma reizinājumu, bet, tā kā strāva un spriegums ir mainīgi lielumi, tad arī jauda būs mainīga.Šajā gadījumā mēs varam noteikt jaudas vērtību katram laika momentam, ja mēs reizinām strāvas vērtību ar sprieguma vērtību, kas atbilst konkrētajam laika momentam.

Lai iegūtu jaudas grafiku, mums jāreizina taisnās līnijas segmentu vērtības, kas nosaka strāvu un spriegumu dažādos laikos. Šāda konstrukcija ir parādīta attēlā. 3, a. Pārtrauktā viļņa forma p parāda, kā mainās jauda maiņstrāvas ķēdē, kurā ir tikai induktīva pretestība.

Veidojot šo līkni, tika izmantots šāds algebriskās reizināšanas noteikums: Ja pozitīvo vērtību reizina ar negatīvu, tiek iegūta negatīva vērtība, un, reizinot divas negatīvas vai divas pozitīvas vērtības, tiek iegūta pozitīva vērtība.

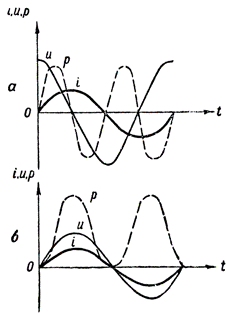
3. attēls. Jaudas grafiki: a — ķēdē, kas satur induktīvo pretestību, b — arī aktīvā pretestība

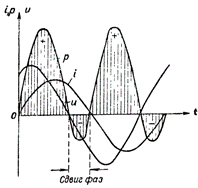
4. attēls. Jaudas diagramma ķēdei, kas satur R un L.

Jaudas līkne šajā gadījumā atrodas virs laika ass. Tas nozīmē, ka starp ģeneratoru un ķēdi nenotiek enerģijas apmaiņa, un tāpēc ķēde pilnībā patērē enerģiju, ko ģenerators piegādā ķēdei.

attēlā. 4 parāda jaudas diagrammu ķēdei, kas satur gan induktīvo, gan aktīvo pretestību. Šajā gadījumā notiek arī apgrieztā enerģijas pārnešana no ķēdes uz strāvas avotu, taču daudz mazākā mērā nekā ķēdē ar vienu induktīvo pretestību.

Pārskatot iepriekš minētos jaudas grafikus, mēs secinām, ka tikai fāzes nobīde starp strāvu un spriegumu ķēdē rada "negatīvu" jaudu.Šajā gadījumā, jo lielāka ir fāzes nobīde starp strāvu un spriegumu ķēdē, jo mazāk strāvas patērēs ķēde, un otrādi, jo mazāka ir fāzes nobīde, jo lielāka ir ķēdes patērētā jauda.

Lasi arī: Kas ir sprieguma rezonanse