Spriegumu, pretestību un jaudu trīsstūri
Ikviens, kam ir priekšstats par vektoru diagrammām, viegli pamanīs, ka tajās var ļoti skaidri atšķirt taisnleņķa sprieguma trīsstūri, kura katra puse atspoguļo: ķēdes kopējo spriegumu, aktīvās pretestības spriegumu un spriegumu. uz pretestību.
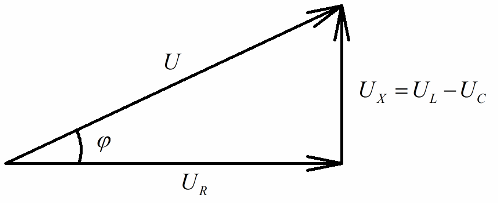
Saskaņā ar Pitagora teorēmu attiecības starp šiem spriegumiem (starp kopējo ķēdes spriegumu un tās sekciju spriegumu) izskatīsies šādi:
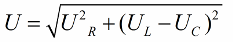
Ja nākamais solis ir sadalīt šo spriegumu vērtības ar strāvu (strāva vienādi plūst cauri visām sērijas ķēdes sekcijām), tad ar Oma likums mēs iegūstam pretestības vērtības, tas ir, tagad mēs varam runāt par taisnleņķa pretestību trīsstūri:
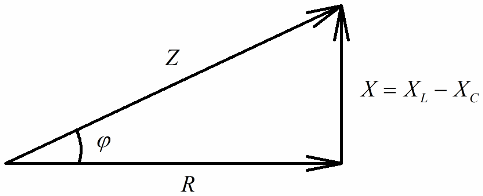
Līdzīgā veidā (tāpat kā spriegumu gadījumā), izmantojot Pitagora teorēmu, ir iespējams noteikt attiecības starp ķēdes pretestību un pretestībām. Attiecības tiks izteiktas ar šādu formulu:
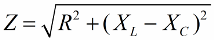
Tad mēs reizinām pretestības vērtības ar strāvu, faktiski mēs palielināsim katru taisnā trīsstūra malu noteiktu skaitu reižu. Rezultātā mēs iegūstam taisnleņķa trīsstūri ar ietilpību:
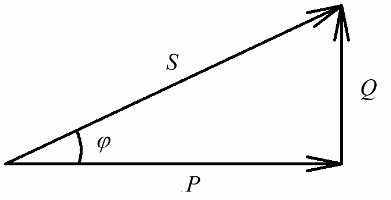
Aktīvā jauda, kas atbrīvota pie ķēdes aktīvās pretestības, kas saistīta ar elektriskās enerģijas neatgriezenisku pārveidošanu (siltumā, veicot darbu iekārtā), būs skaidri saistīta ar reaktīvo jaudu, kas iesaistīta atgriezeniskā enerģijas pārveidē (izveidē). magnētisko un elektrisko lauku spolēs un kondensatoros) un ar pilnu jaudu, kas tiek piegādāta elektroinstalācijai.
Aktīvo jaudu mēra vatos (W), reaktīvo jaudu — varos (VAR — volt-ampere reactive), kopējo — VA (voltu-ampēros).
Saskaņā ar Pitagora teorēmu mums ir tiesības rakstīt:
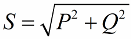
Tagad pievērsīsim uzmanību tam, ka spēka trīsstūrī ir leņķis phi, kura kosinusu ir viegli noteikt galvenokārt pēc aktīvās jaudas un šķietamās jaudas. Šī leņķa kosinuss (cos phi) sauc par jaudas koeficientu. Tas parāda, cik liela daļa no kopējās jaudas tiek patērēta, veicot lietderīgus darbus elektroinstalācijā, un netiek atgriezta tīklā.
Acīmredzot augstāks jaudas koeficients (maksimums viens) norāda uz iekārtas darbībai piegādātās enerģijas augstāku konversijas efektivitāti. Ja jaudas koeficients ir 1, tad visa piegādātā enerģija tiek izmantota darba veikšanai.
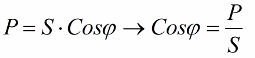
Iegūtie koeficienti ļauj izteikt iekārtas strāvas patēriņu jaudas koeficienta, aktīvās jaudas un tīkla sprieguma izteiksmē:
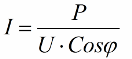
Tātad, jo mazāks ir kosinuss phi, jo lielāka strāva ir nepieciešama tīklam, lai veiktu noteiktu darbu. Praksē šis faktors (maksimālā tīkla strāva) ierobežo pārvades līnijas pārvades jaudu, un tāpēc, jo mazāks jaudas koeficients, jo lielāka ir līnijas slodze un mazāks lietderīgais joslas platums (zems kosinusa phi rada ierobežojumu). Džoula zudumus elektropārvades līnijās ar kosinusa phi samazināšanos var redzēt no šādas formulas:
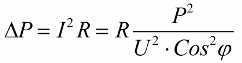
Uz pārvades līnijas aktīvās pretestības R zudumi palielinās, jo lielāka ir strāva I, lai gan tā reaģē uz slodzi. Tāpēc mēs varam teikt, ka ar zemu jaudas koeficientu elektroenerģijas pārvades izmaksas vienkārši palielinās. Tas nozīmē, ka kosinusa phi palielināšana ir svarīgs valsts ekonomiskais uzdevums.
Vēlams, lai kopējās jaudas reaktīvā komponente tuvotos nullei.Lai to izdarītu, būtu labi vienmēr elektromotorus un transformatorus izmantot pie pilnas slodzes un lietošanas beigās tos izslēgt, lai tie nestrādātu tukšgaitā. Bez slodzes motoriem un transformatoriem ir ļoti zems jaudas koeficients. Viens no veidiem, kā palielināt kosinusu phi lietotājiem, ir izmantot kondensatoru bankas un sinhronie kompensatori.
