Strāvu rezonanse

Kondensatora un induktora paralēlais savienojums maiņstrāvas ķēdē

Apsveriet parādības ķēdē maiņstrāvakurā ir paralēli savienots ģenerators, kondensators un induktors. Pieņemsim, ka ķēdei nav aktīvas pretestības.

Acīmredzot šādā ķēdē gan spoles, gan kondensatora spriegums jebkurā brīdī ir vienāds ar ģeneratora izstrādāto spriegumu.

Kopējā strāva ķēdē sastāv no strāvām tās atzaros. Strāva induktīvā atzarā atpaliek no sprieguma fāzē par ceturtdaļu perioda, un strāva kapacitatīvā atzaro to ved par to pašu perioda ceturksni. Tāpēc strāvas zaros jebkurā laika momentā izrādās fāzes nobīdītas viena pret otru par pusi perioda, tas ir, tās ir pretfāzē. Tādējādi strāvas zaros jebkurā brīdī ir vērstas viena pret otru, un kopējā strāva ķēdes nesazarotajā daļā ir vienāda ar to starpību.

Tas dod mums tiesības uzrakstīt vienādību I = IL -integrālā ķēde

kur es- kopējās strāvas efektīvā vērtība ķēdē, I L un integrālā shēma — strāvu efektīvās vērtības zaros.

Izmantojot Oma likumu, lai noteiktu strāvas efektīvās vērtības zaros, mēs iegūstam:

Il = U / XL un Az° C = U / XC

Ja ķēdē dominē induktīvā pretestība, ti. XL Vairāk ▼ XC, strāva spolē ir mazāka par strāvu kondensatorā; tāpēc strāvai ķēdes nesazarotajā daļā ir kapacitatīvs raksturs un ķēde kopumā ģeneratoram būs kapacitatīva. Un otrādi, ja XC ir lielāks par XL, strāva kondensatorā ir mazāka par strāvu spolē; tāpēc strāva ķēdes nesazarotajā daļā ir induktīva, un ķēde kopumā ģeneratoram būs induktīva.

Nedrīkst aizmirst, ka abos gadījumos slodze ir reaktīva, t.i. ķēde nepatērē ģeneratora jaudu.

Strāvu rezonanse

Tagad aplūkosim gadījumu, kad paralēli savienotais kondensators un spole izrādījās vienādi pēc to pretestības, t.i. XlL = X°C.

Ja tāpat kā iepriekš pieņemam, ka spolei un kondensatoram nav aktīvās pretestības, tad, ja to reakcijas ir vienādas (YL = Y° C) ķēdes nesazarotajā daļā kopējā strāva būs nulle, savukārt zaros vienāda straumes plūdīs ar vislielāko stiprumu. Šajā gadījumā ķēdē notiek rezonanses strāvu parādība.

Pie strāvas rezonanses strāvu efektīvās vērtības katrā atzarā, ko nosaka ar attiecībām IL = U / XL un Аz° С = U / XC, būs vienādas viena ar otru, lai XL = XC.

Secinājums, ko nonācām, no pirmā acu uzmetiena var šķist diezgan dīvains. Faktiski ģenerators ir noslogots ar divām pretestībām un ķēdes nesazarotajā daļā nav strāvas, savukārt pašās pretestībās plūst vienādas un turklāt lielākās strāvas.

Tas izskaidrojams ar spoles magnētiskā lauka uzvedību un kondensatora elektriskais lauks… Pie strāvu rezonanses, kā sprieguma rezonanse, pastāv enerģijas svārstības starp spoles lauku un kondensatora lauku. Šķiet, ka ģenerators pēc enerģijas paziņošanas ķēdei ir izolēts. To var pilnībā izslēgt, un strāva ķēdes sazarotajā daļā tiks uzturēta bez ģeneratora ar enerģiju, ko ķēde sākotnēji uzglabā. Arī spriegums ķēdes spailēs paliks tieši tāds pats kā ģeneratora izstrādātais spriegums.

Tādējādi, paralēli savienojot induktors un kondensators, mēs ieguvām oscilatora ķēdi, kas atšķiras no iepriekš aprakstītās tikai ar to, ka ģenerators, kas rada svārstības, nav tieši savienots ar ķēdi un ķēde ir slēgta. 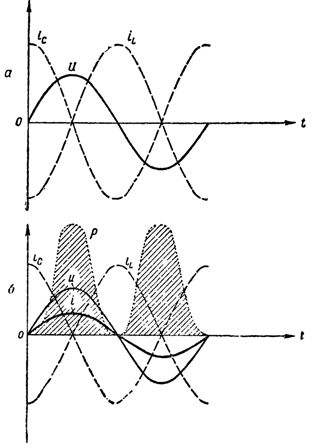Strāvu, sprieguma un jaudas diagrammas ķēdē pie strāvu rezonanses: a — aktīvā pretestība ir vienāda ar nulli, ķēde nepatērē enerģiju; b — ķēdei ir aktīva pretestība, ķēdes nesazarotajā daļā ir parādījusies strāva, ķēde patērē enerģiju

L, C un e, pie kurām notiek strāvas rezonanse, tāpat kā sprieguma rezonansi (ja neņemam vērā ķēdes aktīvo pretestību) nosaka ar vienādību:

ωL = 1 / ω° C

Tāpēc:

eres = 1/2π√LC

Lres = 1 / ω2C

Gabals = 1 / ω2L

Mainot jebkuru no šiem trim lielumiem, var panākt vienādību Xl = X° C, t.i., ķēdi pārvērst par oscilējošu ķēdi.

Tātad, mums ir slēgta svārstību ķēde, kurā mēs varam izraisīt elektriskās svārstības, t.i. maiņstrāva. Un, ja nebūtu aktīvās pretestības, kas piemīt katrai oscilējošai ķēdei, tajā varētu nepārtraukti pastāvēt maiņstrāva.Aktīvās pretestības klātbūtne noved pie tā, ka svārstības ķēdē pakāpeniski samazinās, un to uzturēšanai ir nepieciešams enerģijas avots - ģenerators.

Nesinusoidālās strāvas ķēdēs ir iespējami dažādu harmonisko komponentu rezonanses režīmi.

Rezonanses strāvas tiek plaši izmantotas praksē. Strāvas rezonanses fenomens tiek izmantots frekvenču joslas filtros kā elektriskā "skava", kas aizkavē noteiktu frekvenci. Tā kā frekvencē f ir ievērojama strāvas pretestība, sprieguma kritums ķēdē pie frekvences f būs maksimālais. Šo cilpas īpašību sauc par selektivitāti, to izmanto radio uztvērējos, lai izolētu konkrētas radiostacijas signālu. Viena no galvenajām sastāvdaļām ir svārstību ķēde, kas darbojas strāvu rezonanses režīmā elektroniskie ģeneratori.